Feed Back

Friday, May 05, 2006

e

$e$ ，作为数学常数，是自然對數函數的底數。有時稱它為欧拉数（Euler number‎），以瑞士數學家歐拉命名；也有個較鮮見的名字納皮爾常數，以紀念蘇格蘭數學家約翰·納皮爾引進對數。它的數值約是（小數點後100位）：

e

≈ 2.71828 18284 59045 23536 02874 71352 66249 77572 47093 69995 95749 66967 62772 40766 30353 54759 45713 82178 52516 64274

就像圓周率π和虛數單位i， $e$ 是數學中最重要的常數之一。它有幾種等價定義，下面列出一部份：

定義

最常見的四種 $e$ 的定義如下：

1. 定義e 為下列極限值：

$e = \lim_{n\to\infty} \left(1+\frac{1}{n}\right)^n$ 。

2. 定義e為下列无穷级数之和：

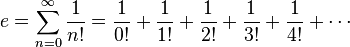$e = \sum_{n=0}^\infty {1 \over n!} = {1 \over 0!} + {1 \over 1!} + {1 \over 2!} + {1 \over 3!} + {1 \over 4!} + \cdots$ ，

其中n!表n的階乘。

3. 定義

e

為唯一的數

x > 0

使得

$\int_{1}^{x} \frac{1}{t} \, dt = {1}$ 。

4. 定義

e

為唯一的數使得

$\lim_{h\to 0}\frac{e^h-1}{h}=1$

這些定義可證明是等價的。

性質

很多增長或衰減過程都可以用指數函數模擬。指数函数 $e x$ 重要在它是唯一的函數與其導數相等（乘以常數，最一般的函數形式為 $k e x$ ， $k$ 為任意常數）。

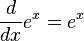$\frac{d}{dx}e^x=e^x$ 。

e是無理數和超越數（見林德曼—魏爾施特拉斯定理(Lindemann-Weierstrass)）。這是第一個獲證為超越數，而非故意構造的（比較劉維爾數）；由夏爾·埃爾米特(Charles Hermite)於1873年證明。有猜想它為正規數。它出現在數學中一條很重要的等式，稱為欧拉公式：

$e^{ix} = \cos\,x + i\sin\,x \,\!$ 。

當 $x = π$ 的特例是歐拉恆等式：

$e^{i\pi} + 1 = 0 \,\!$ ，

這式被理查德·費曼稱為「歐拉的寶石」。

$e$ 的無窮連分數展開式有個有趣的模式，可以表示如下：

$e = [1; 0, 1, 1, 2, 1, 1, 4, 1, 1, 6, 1, 1, 8, 1, 1, 10, 1, 1, 12,\ldots] \,$ 。

無理數證明

證明 $e$ 是無理數可以用反證法。假設 $e$ 是有理數，則可以表示成 $a / b$ ，其中 $a, b$ 為正整數。以 $e$ 的無窮級數展開式可以得出矛盾。

考慮數字

$x = b\,! \left(e-\sum_{i=0}^b {1 \over n\,!}\right)$ ，

以下將推導出 $x$ 是小於1的正整數；由於不存在這樣的正整數，得出矛盾，所以得證 $e$ 是無理數。

$x$ 是整數，因為

$0 < x = b\,! \left(e - \sum_{i=0}^b {1 \over n\,!}\right) = b\,! \left({a \over b} - \sum_{i=0}^b {1 \over n\,!}\right)$

$= a (b-1)! - \sum_{n=0}^b {b\,! \over n\,!}$

$= a (b-1)! - \left(1 + \sum_{n=0}^{b-1} b(b-1)\cdots(n+1)\right)$ 。

$x$ 是小於1的正數，因為

$0 < x = b\,! \sum_{n=b+1}^\infty {1 \over n!}$

$= \frac{1}{b+1} + \frac{1}{(b+1)(b+2)} + \frac{1}{(b+1)(b+2)(b+3)} + \cdots$

$< \frac{1}{b+1} + \frac{1}{(b+1)^2} + \frac{1}{(b+1)^3} + \cdots = {1 \over b} < 1$ 。

歷史

第一次提到常數 $e$ ，是約翰·納皮爾於1618年出版的對數著作附錄中的一張表。但它沒有記錄這常數，只有由它為底計算出的一張自然對數列表，通常認為是由威廉·奧特雷德(William Oughtred)製作。第一次把e看為常數的是雅各·伯努利(Jacob Bernoulli)，他嘗試計算下式的值：

$\lim_{n\to\infty} \left(1+\frac{1}{n}\right)^n$ 。

已知的第一次用到常數 $e$ ，是莱布尼茨於1690年和1691年給惠更斯的通信，以b表示。1727年歐拉開始用 $e$ 來表示這常數；而 $e$ 第一次在出版物用到，是1736年歐拉的《力學》(Mechanica‎)。雖然往後年日有研究者用字母c表示，但 $e$ 較常用，終於成為標準。

用e表示的確實原因不明，但可能因為 $e$ 是「指數」(exponential‎)一字的首字母。另一看法則稱a，b，c和d有其他經常用途，而 $e$ 是第一個可用字母。不過，歐拉選這個字母的原因，不太可能是因為這是他自己名字Euler‎的首字母，因為他是個很謙虛的人，總是恰當地肯定他人的工作。

e在數學外的用途

在Google2004年的首次公開募股，集資額不是通常的整頭數，而是$2,718,281,828，這當然是取最接近整數的 $e$ 十億美元。（顺便一提，Google2005年的一次公開募股中，集資額是$14,159,265，与圆周率π有关）
Google也是首先在矽谷心臟地帶，接著在麻薩諸塞州劍橋出現的神祕廣告版的幕後黑手，它寫著{first 10-digit prime found in consecutive digits of e}.com（在e的連續數字中第一個發現的十位質數.com）。解決了這問題（第一個 $e$ 中的十位質數是7427466391，出奇地到很後才出現，由第100個數字開始），進入網站後還有個更難的題目要解決，最後會到達Google的招聘頁。但這個挑戰已結束，上述網站都已關閉。
著名计算机科学家高德納的書METAFONT的版本號碼趨向 $e$ （就是說版本號碼是2，2.7，2.71，2.718等）。

参见

您可以在维基文库中查找此百科条目的相关原始文献：E的前十万位

无理数
欧拉数
圆周率
在維基文庫中的：E的前十万位

Feed Back

Friday, May 05, 2006

e

目录

定義

性質

無理數證明

歷史

e在數學外的用途

参见

Archives

About Me